Oczywiście nie chodzi wyłącznie o sam fakt poruszania nią. Naukowcy mieli w kontekście tego zagadnienia konkretny cel: ustawić igłę tak, aby zajmowała jak najmniej miejsca. I choć pierwsze próby dokonania przełomu nastąpiły jeszcze przed końcem pierwszej wojny światowej, to matematycy przez całe dekady nie doprowadzili do sytuacji, w której mogliby ogłosić przełom.
Czytaj też: Przełom w matematyce! Powstał nowy sposób poszukiwania liczb pierwszych
W tym roku pokusił się o to jednak duet naukowców. W związku z tym głównymi bohaterami tej wiadomości będą Hong Wang z New York University i Joshua Zahl z University of British Columbia. Jak sugerują inni badacze, chodzi o jedno z najważniejszych osiągnieć matematycznych XXI wieku. Takie słowa padły w reakcji na udowodnienie trójwymiarowej wersji hipotezy Kakeyi.
Obracająca się igła to główny element zagadki matematycznej, której autorem był Sōichi Kakeya
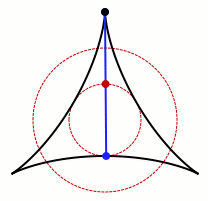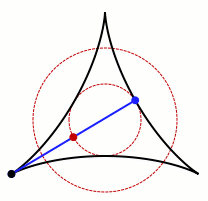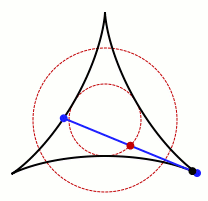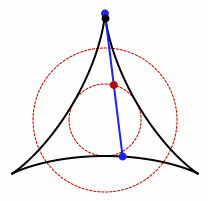
Mając do dyspozycji nieskończenie wąską igłę, którą chcemy obrócić o 360 stopni – z założeniem, że musi ona wskazywać w każdym kierunku płaszczyzny przynajmniej raz – po prostu obrócimy ją tak, by pokryła powierzchnię koła. Jest to proste w realizacji, nawet jeśli na podstawie powyższego opisu niekoniecznie jesteście w stanie sobie to zwizualizować. Niestety, im dalej w las, tym więcej komplikacji.
A to w związku ze wspomnianym Japończykiem, który postawił sobie za cel obracanie igły tak, aby zajęła jak najmniej miejsca. Poprzez poruszanie nie tylko końcami igły, ale również jej środkiem, Kakeya zamiast koła stworzył trójkąt wyznaczony przez obracającą się igłę. Ten wariant możecie zobaczyć na przedstawionej animacji. Dodatkowo, środek igły utworzył niewielkich rozmiarów koło umieszczone w centrum.
Później sprawą zainteresował się kolejny mistrz w swoim fachu: Abram Besicovitch. Jego udział w matematycznym śledztwie również był istotny, ponieważ Besicovitch wykazał, że igłę można przesuwać tak, aby pokryta przez nią powierzchnia miała całkowitą powierzchnię zerową. To doprowadziło do postawienia pytania: jaka jest powierzchnia Kakeyi?
Czytaj też: Teoria matematyczna tak skomplikowana, że zrozumiało ją tylko 20 osób na świecie
Zwykle, gdy mówimy o płaszczyźnie, odpowiedź brzmi: dwuwymiarowa. Ale czasami zdarzają się wyjątki, ponieważ na przykład fraktale mogą być 1,5-wymiarowe. W 1971 roku Roy Davies ogłosił, iż powierzchnia Kakeyi jest zawsze dwuwymiarowa, nawet przy zerowej powierzchni całkowitej. A czy jeśli igła będzie obracana wzdłuż wszystkich n kierunków przestrzennych, to zawsze pokryje n-wymiarową objętość?
Długo wyczekiwanej odpowiedzi udzielili autorzy najnowszych doniesień, czyli wspomniani Wang i Zahl. W toku swoich działań odrzucili wszystkie scenariusze, w którym uzyskana objętość miałaby wymiar mniejszy niż trzy. To z kolei oznacza, że udowodnili hipotezę Kakeya w trzech wymiarach przestrzennych, co zdaniem komentatorów może doprowadzić do szeregu przełomowych ustaleń w dziedzinie matematyki.